We’ve built ourselves a positive case for "Many More Much Smaller Steps" (MMMSS). There’s a counter-case, tho, based in a trio of proposed optimizations. Sadly, those optimizations usually flop. Today, let’s take up the "Shortest Distance" floptimization.
Many More Much Smaller Steps – First Sketch | GeePawHill.org
The first plank of my take on fixing the trade is MMMSS: If you want more value faster, take Many More Much Smaller Steps. Today I want to start laying this out for folks. This isn’t gonna happen in o…
Folks, I love thinking & writing & talking about geekery, and I hope you do, too. But before we start, I want to say that social justice is a far more important issue to me than anything in geekery. Please keep working for & supporting change. Black Lives Matter.
The counter-case to MMMSS is supposed to be a set of optimizations — ways around the odd disorderly-seeming path forced on us by stride-limits. They are compelling, these optimizations. But false. I call them "floptimizations".
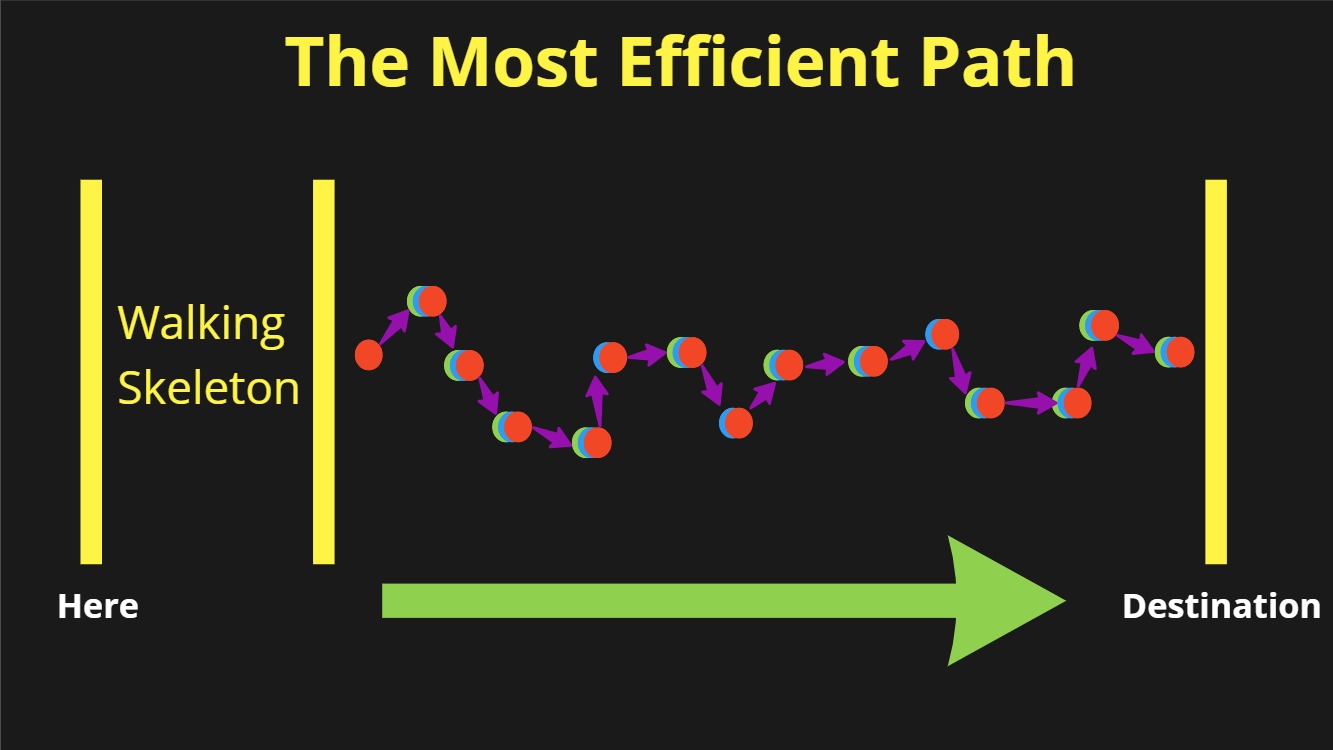
The shortest-distance floptimization says "We’ll go faster if we aim perfectly and head right to the target." It’s a straightforward application of 2d plane geometry. It’s one of the first things we learn in school: the shortest distance between two points is a straight line!
Graphically, it looks like this. We replace the strange wandering MMMSS steps with a single large step — a straight line — from where we are now to where we wish to go.
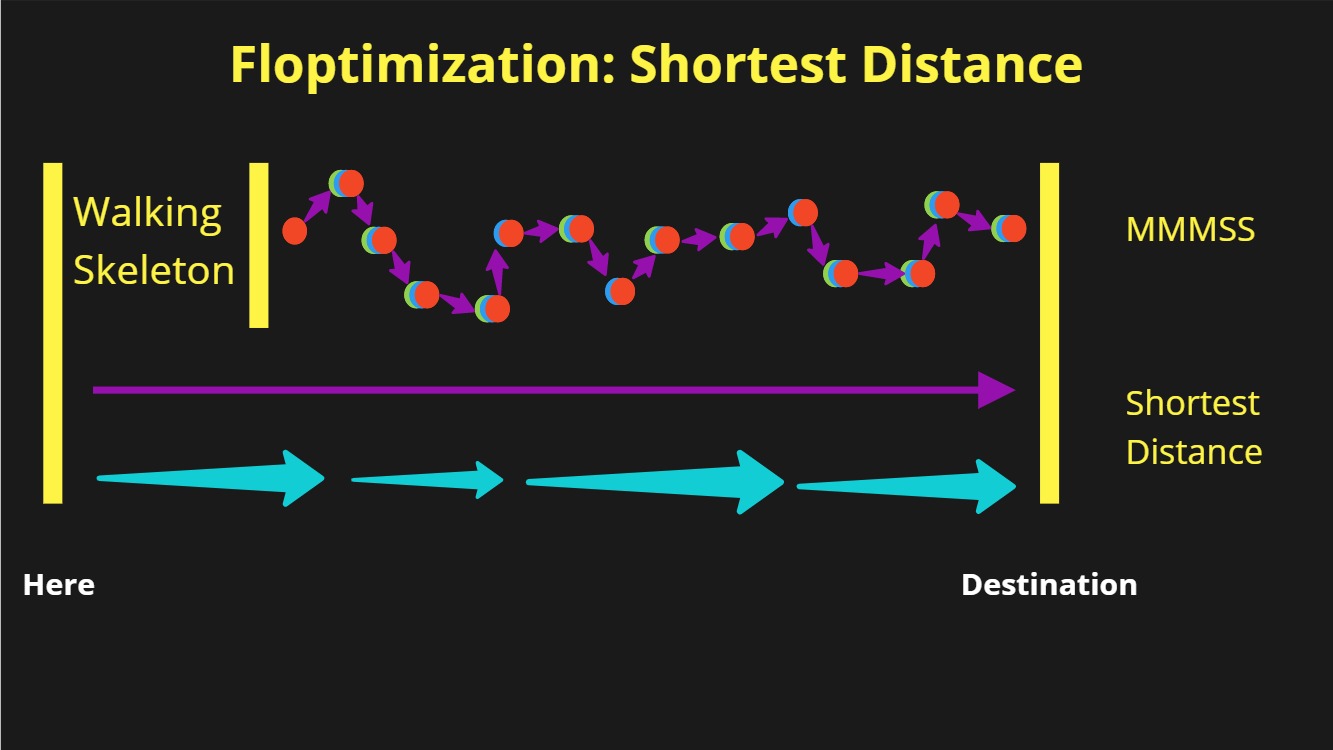
The common variation of this is to break that very long step into a sequence of actions, each of which is a different activity, but none of which is a step, because it doesn’t start ready and end ready. This is sleight-of-hand, it’s still one gigantic step.
So, looking at these images, it certainly seems like this optimization would help. Why, then, does it flop so often? For these reasons: 1) Perfect aiming is expensive and risky. 2) Big steps lack intrinsic step-benefit. 3) Business doesn’t take place on a two-dimensional plane.
Start by considering the cost of better aim: It costs effort to improve one’s aim, real time and real energy and real money. That cost is rarely factored into calculating the would-be benefit of the shortest-distance floptimization.
We’ve all seen the situation where a product owner proposes a seemingly minor change, and the team responds by saying that it could certainly be done and will take only three months to accomplish.
Blammo.
Why’s this happen and what does it mean?
Modern applications are built from many parts, some of which we control perfectly, others of which we bought and installed. And each of these parts carries with it a set of decisions, assumptions about how it can and will be used.
Now, no given part’s decision-assumptions are all that onerous or constraining. When we put them all together, though, we’re talking about dozens and dozens of them, arranged rather just so, quite delicately. The level of intricacy and complexity is staggering.
Two proposed changes, side by side, may seem to an outsider to be almost identical in scope. But one of these could take 15 minutes to implement, and the other could take 15 weeks.
It’s because one of them fits the pre-made assumptions, and the other one doesn’t.
(In real-life, it can also happen that we purposefully built our own parts so that changing them is inherently expensive. That’s the subject of the third plank: "Develop change-enabling technique." But even in theory, with perfect code & coders, this will still happen.)
We make hundreds, even thousands, of these decisions. One thousand decisions, each with 99% accuracy, virtually guarantee an error. And at this level of avoiding change-blockers, a miss is as good as a mile.
(Shouts out to Grandma, for one of her less profane sayings.)
That is, a 95% aiming accuracy is only slightly better than an 80% accuracy at avoiding these situations. To have aim truly and reliably back this floptimization, we need to be well past 99%.
And that, my friends, is a difficult and expensive propositon, maybe even impossible.
Furthermore, because the steps are so large, the cost of each step is large, which means the cost of making a mistake in one of those decisions is far higher than with small steps, even as the cost of perfecting our aim also grows wildly.
So the cost & risk of near-perfect aim is staggeringly high in the real world, but it’s invisible in the case for the shortest-distance floptimization.
Next, we have the loss of step benefit: In an earlier article, we discussed the considerable intrinsic benefit of small steps, the value they bring for no other reason than that they are small steps. When we apply the shortest-distance floptimization, we lose nearly all of it.
The eight benefits we listed were interruptability, steerability, reversability, target parallelism, scope, rhythm, safety, and autonomy.
Tho each one isn’t equally present in every small step, there are usually several in play, and taken together, they add up to a lot.
Some of these benefits simply disapper entirely when we take the shortest-distance floptimization. For instance, scope is right out the door: the larger step absolutely requires much larger mental scope. Similarly for steerability and interruptability.
Of course, our emphasis on aim will also reduce both autonomy and safety. The former, because our aim has to describe our result in such high detail there’s little room for maneuver. The latter, because the size of the step relates directly to the size of the risk.
Finally, we have non-planar business reality: though the abstraction and images represent and reason from a 2d plane, neither software development nor business itself hold to Euclidean geometry. The metaphor simplifies the reality so much it becomes useless to us.
Far from being a plane, professional software development takes place on an incredibly twisty, complicated, loopy, ever-shifting, high-dimensional, murky, and curved manifold, one we call "reality". We actually know the first rebuttal here, and can illustrate it trivially:
Diet Coke is a kind of security blanket for me, helping me cope. When my supplies run out, my nearest source is my local country store, Ashley’s Market.
Think where your nearest source is, in case I come to visit.
Measured in a straight line, the distance from here to Ashley’s is only 1 mile. Seen on the plane, that’s the obvious shortest distance, but believe me when I tell you that it would be both inefficient and highly dangerous for me to take that route.
There’s two stories down to the ground, then two ravines down and up again on a 30 degree grade, with a more shallow ravine between, holding a river for me to wade across, and — country living — many armed neighbors who aren’t fond of trespassers, then finally, a highway.
And for you? Imagine I’ll be arriving in half an hour. If you drew a straight line between where you are and where the nearest Diet Cokes can be had?
I’m guessing that, for the overwhelming majority, you’d have a similarly difficult time traversing that straight line.
(Hopefully one with fewer armed property-owners, I realize many of my readers live in places where this isn’t a risk.)
Taking the two-mile route I take every few days is far preferable. Trivially, then, "shortest distance" does not equate to efficiency or effectiveness or even — good lord — safety.
But that’s a pot-shot rebuttal, really. There’s better.
Because, in that cheap rebuttal, me, Ashley’s and the route are all both known and stable. (Well, stable-ish, I do have my moods.) But in software development, the code, the target, and the route between the two undergo far more frequent change.
The target in the business world moves almost continuously. Markets are volatile, and we don’t own our competitors or our customers either one. I’ve worked with teams whose business domain — b2b — couldn’t let them reliably aim further out than two days at a time.
And even in semi-stable business domains, I’d bet all of you who’ve been in the trade longer than a year have experienced at least one or two dramatic target-shifts. It is absolutely routine in software development: the target moves, and this is normal.
Of course, when the target moves, the route changes. In fact, the route changes anyway, even when the target stands relatively still.
Why? Because "the route" isn’t a universal objective permanent line on a flat map. It’s local to our team & its vision, and changes as they do.
Our routes are based very heavily in our tech and our mindset, because we do creative, collaborative and technical work for a living. Problems can be very similar and still have very different routes to their solution, it happens all the time.
You see, in the geek trades, they don’t pay us to solve problems we’ve already solved for them. I know the route to Ashley’s because I’ve been there a thousand times.
Have you been to your software solution a thousand times?
No, there isn’t a known route, and we don’t follow it. There is an expectation that a route exists, and we discover and elaborate it — as we go. The route is no more stable than the target itself.
And finally, there’s the code.
The code moves, like I do, between where it’s at now and where it’s going. But unlike me, it changes a lot as it moves. When we move code from here to there, by definition, we’re driving a self-modifying car.
So you can see, with all this change, the concepts from the 2d plane are really not terribly applicable. If we base our logic in the Euclidean context, we’re ignoring critical factors that apply in our own actual context.
The upshot, of aiming cost, loss of step-benefit, and non-planar business reality:
The reasoning in the shortest-distance floptimization is simple, direct, almost physical, and its absolutely ubiquitous in our trade.
But it’s a floptimization.
Does it ever apply? Of course! There are situations in which our aim truly can be extraordinarily accurate at low cost. Usually these are situations where our horizon goal isn’t more than a few steps away, is well-understood, and is close to a problem we’ve solved before.
Such situations certainly benefit from applying shortest-distance reasoning.
But.
The key is in understanding how occasional these situations really are.
Say a shortest-distance approach works 10% of the time. (That’s a figure I suspect is far too high in real life, but go with me here.)
One time in ten, we find ourselves in a situation where this effort is truly optimal.
It’s a terrific approach to take every situation and cheaply probe it to see if it qualifies for that optimization.
It’s a terrible approach to take every situation and assume that it qualifies for that optimization.
And that’s what the trade actually does.
So think about it.
We set out to optimize our wonky crooked stride-limited path to a horizon. We used the straightforward — heh, see what I did there? — metaphor of the shortest distance. Did we get a stable, reliable, high-probability optimization?
We did not.
In coming days, we’ll consider 1) "Pin-making", where we create specialists, stations, and handoffs, and 2) "Mastermind", where we create a centralized intelligence to control our operations. As we’ll see, these, seemingly brilliant, aren’t particularly effective, either.
Phew. A long one. Thanks for hanging in to the end. I took a long break in writing muses, and it took me a while to pull my notes together for this one. Next one maybe will happen a little sooner.
Does the GeePaw Blogcast add value?
If so, consider a monthly donation to help keep the content flowing. You can also subscribe for free to get weekly posts sent straight to your inbox. And to get more involved in the conversation, jump into the Camerata and start talking to other like-minded Change-Harvesters today.